Quantum Photonics
Building the future of quantum communications by developing integrated optics technologies.
Quantum Random Number Generation
What is a Quantum Random Number Generator?
Quantum Random Number Generators (QRNGs) generate random numbers by means of physical processes rather than algorithms. They use the inherent randomness of quantum mechanics to produce random numbers. Quantum randomness is information-theoretically provable and passes existing benchmarks like the National Institute of Standards and Technology (NIST) test for randomness.
Why QRNG?
True random numbers play a vital role in fields of science, technology, and industry. While every other form of randomness can be influenced by hidden variables, quantum randomness is entirely unpredictable by nature. Having full knowledge of the initial conditions of a classical random number generator can help you predict the output, which can be detrimental in fields like cryptography, for instance. Visit our Online QRNG to use our QRNG and request quantum random bits generated in real time.
Toeplitz Hashing
In a QRNG, a quantum state is prepared and a measurement is then taken on the state. However, because of imperfections in the experiment, the quantum signal is inevitably mixed with classical noise. Thus, the QRNG requires some post-processing in order to extract the true randomness and eliminate the contributions of said noise. In our experiment, we use a Toeplitz hash extraction algorithm to process the raw data. Because our raw data follows a random Gaussian distribution (some numbers are more likely than others), the goal of this hash extraction is to suppress the classical contributions and construct a uniform distribution of our random data.
The procedure of Toeplitz hashing starts with a raw data sample of size n (produced by the measurement of the quantum state) with a min-entropy of k (the lower bound on its randomness) and a security parameter ε. For example, if we start with an input bit-length of 8 and our min-entropy is 6.7, we can extract 6.7 random bits per 8 bits of raw data, or 80%. With this information, we can find the output length, m. We then construct a Toeplitz matrix with an n + m - 1 random-bit seed and multiply this matrix with the raw data to produce the extracted uniform data.
Raw data before Toeplitz hashing:

Extracted data after Toeplitz hashing:

On-Chip QRNG
On-chip QRNG has been done before; however, what makes this project unique is that we use a 90° optical hybrid. Optical hybrids, or coherent receivers, are common in industry and are often used for classical communication, but we use it in QRNG so we can measure something other than the vacuum state as the input. In future research, optical hybrids can enable more efficient quantum tomography because it gives us conjugate pairs of quadrature data.
Theory
Quantum randomness bodes more success when we can use small signals on the order of 10 photons. Because light levels that low are extremely difficult to detect, we use a 90° optical hybrid circuit. This circuit interferes with the signal we want to measure with a stronger known signal called a local oscillator. The four outputs of this circuit can be used to reconstruct our original unknown signal and measure its randomness.
Optical Hybrid
A 90° optical hybrid is a six-port optical device with two inputs—a signal of unknown amplitude and phase and a stronger reference signal of known amplitude and phase—and four outputs. The reference signal interferes with the unknown signal, and a multi-mode interferometer (MMI) splits and interferes the signal with the reference. At a certain range of frequencies, the phase-relationship between the signal and the reference of each of the four outputs measure 90° away from each other and is shown below. These outputs are the necessary inputs for conjugate homodyne detection.

The X and P pairs are sent into two balanced detectors and the RF outputs are measured. We then take the sum of the squared outputs of the two balanced detectors to get Z, which is proportional to the photon number of the original unknown input state. After many measurements, we can build photon number statistics and, using quantum tomography, can completely reconstruct the original unknown quantum state.
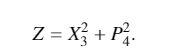
On-Chip CV-QKD
With data privacy being an ever increasing concern, advancements in quantum safe cryptography is vital. One promising protocol that is proven to be quantum safe is quantum key distribution (QKD). We are exploring this protocol in the continuous variable (CV) regime. By integrating the quantum devices required to realize such a scheme in silicon photonics, we can minimize costs while allowing for scalability.
Quantum Simulation
Accurate simulations are essential to predict how a circuit will function before you spend thousands of dollars fabricating a chip. Many packages, including Simphony and SiPANN created by our computational photonics team, already provide accurate simulations of integrated photonic circuits. However, to our knowledge, no widely available simulator can account for the quantum properties of integrated photonic circuits.
Most RF and photonic circuit solvers model all circuit components using compact models with each component's scattering parameters. These parameters encode the amplitude and phase transfer functions for each compact model, which are then concatenated using sub-network growth algorithms. For passive quantum circuits with Gaussian inputs, we can define an analogous quantum model using unitary operations based on the parameters. These operators act on a vector of means and a matrix of covariances, which represent a Gaussian state.
We demonstrate this method by first simulating an idealized yet non-trivial quantum circuit using both Strawberry Fields, an existing open-source quantum simulator, and our new scattering parameter formulation implemented using the open-source Simphony package. An example is shown in the figure below.

Entangled Photon Pair Sources
Integrated Sources
Quantum networks promise a future of completely secure communication, and entangled photon pairs are their message carriers. Most entangled photon pair sources use free space optics which require more space and maintenance (e.g. aligning) while integrated sources are compact and can be mass-produced. We're designing novel integrated EPPSs, including narrow frequency-band and polarization entangled sources.
Phase-Matched Structures
Our sources use Spontaneous Parametric Down-Conversion, a nonlinear optical process, to generate the photon pairs. Quasi-phase matching (QPM) is crucial for large output powers/high pair counts. The most common way to do QPM is by periodic poling of waveguides or rings. For some of our designs we use the conventional poling method, as it is a widely established technique in terms of theory. However, periodic poling is both difficult to carry out in fabrication and it restricts the types of structures we can use. Therefore, to relax the constraints on fabrication and structure options we are developing a new method for making integrated photonic structures that are phase-matched for specific nonlinear processes without needing to use periodic poling. This is accomplished through the use of topology optimization and adjoint gradient solving through MEEP.

Quantum Emitters
Color centers are single or few-atom defects in a crystal that are used to store qubits while waiting for other operations to finish or signals to arrive. They are quantum "memories" similar to memory in classical computers. To store and retrieve the information stored in the color center with high chance of success, it must be stimulated by a pulse of light with a very specific wavelength which causes it to emit a photon that carries the qubit. This can be done by putting the color center in a resonant cavity to modify the quantum density of states to restrict the bandwidth of the emission wavelength. However, resonant cavities are not particularly good at emitting photons into specific directions, making extracting the qubit photons from the cavity difficult.
We are designing resonator cavities that solve both of these problems through the use of photonic design and topology optimization. These memories are planned to be used in quantum networks developed by the Center for Quantum Networks research center.
Green Machine
Motivation
The efficiency of classical communication systems is heavily dependent on the strength and clarity of an incoming signal at the receiver. Error correcting code (ECC) can help in some situations to increase or simply maintain information efficiency at great distances. However, these classical systems struggle in photon starved environments. Examples of such environments might include deep space communication applications or even a direct Earth-to-Mars communication link with a rover on Mars’ surface.
Current technologies can require exorbitant amounts of power to send a strong enough signal to be clearly received. However, we are developing a device that leverages the quantum nature of light to send and receive data long distances more efficiently in low photon environments than any other existing technology today. In fact, our device beats the ideal information efficiency limit for any classical receiver in low photon environments.
Theory
The most useful encoding system in low photon environments is Pulse Position Modulation (PPM). It’s efficient and has a low error rate. However, when sending such a pulse, we have to make sure the output power is high enough such that the received signal is above some minimum power threshold or noise floor. Consider that over great distances we may receive on average less than one photon per pulse. If we look at any form of Quadrature Amplitude Modulation (QAM) above 4-QAM where amplitude plays a large role in encoding information, it becomes evident how PPM has a significant advantage.
However, sending QAM signals is much simpler. The Greene Machine (GM) is a device which performs a transformation on a received signal that converts it from QAM to PPM.
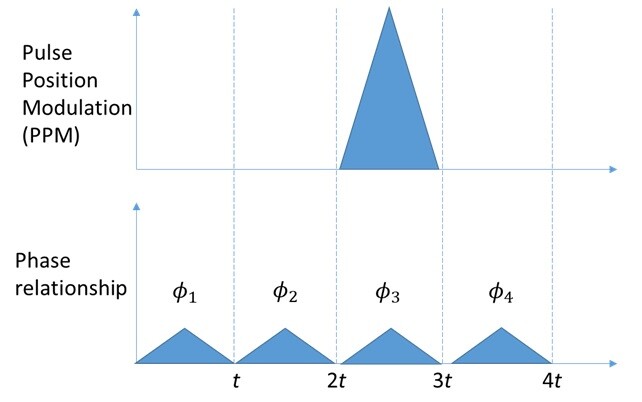
Figure 1. Pulse position modulation demonstrated in time bins compared with our proposed method of sending a pulse in each time bin, each with a relative phase relationship.
Consider an n-bit binary phase-shift keyed (BPSK) “codeword.” Using PPM, each codeword would only have one of the n bits “active,” corresponding the information to be transmitted. Instead of attempting to send a pulse in the correct time bin (which would require not only a synchronized clock on the transmitting and receiving end, but also the ability to receive such a clear signal—the same challenge as with classical devices), we propose sending some signal in each time bin, but with a relative phase change between each time bin (see Figure 1).

Figure 2. Various input codewords with their relative phases, the Green Machine architecture, and the resulting outputs [1].
As mentioned above, the Green Machine is an architecture that performs a linear transformation on an incoming signal. Supposing we use some binary phase-shift keyed (BPSK) encoding system, as illustrated by the received codewords in Figure 2, the GM performs a linear transformation that converts these linearly independent, maximally orthogonal BPSK codewords into a linearly independent basis with PPM encoding. We see that the codewords both on the input and output sides of the transformation are a basis for their respective codespaces.
Therefore, instead of sending a pulse in a single time bin corresponding to the bit we’d like to transmit, we can send a pulse in every time bin, each with a relative phase relationship. On the receiving side, we can send each pulse to its own channel (perhaps with time demultiplexing) and allow each codeword to travel simultaneously through the GM architecture. The signals comprising the codeword are then allowed to interfere with each other throughout the GM structure. Even though each channel receives on average less than one photon, since the photon is not observed or detected until it has passed through the architecture (using perhaps a single photon detector), due to the quantum nature of light (namely, the principles of superposition and uncertainty), we can receive on average one photon with a very high probability of appearing at the correct PPM encoded output port.
Implementation

Figure 3. Diagram and actual construction demonstrating how light travels through the green machine free-space setup from the fiber launch (FL), interfering through beam splitters (BS), reflecting off mirrors (M), and returning to the photodiodes (PD).
We were able to implement a 4-port version of this device in free-space [2]. Previous research has demonstrated that it is possible to characterize devices whose codewords are not ideal (not maximally orthogonal) due to errors in fabrication such as path length differences. Even so, each codeword is distinct enough from the other codewords to allow for efficient encoding or decoding.
Current Work

Figure 4. One of the green machine integrated photonic chips we currently perform our experimentation on.
We are in the process of replicating the free-space results on an integrated photonic chip. Using precision alignment techniques, we can test these cleanroom-fabricated chips and run the same algorithms as were used on the 4-channel free space setup to characterize these 8-channel photonic circuits and learn their codewords.
Sources
Saikat Guha. “Structured Optical Receivers to Attain Superadditive Capacity and the Holevo Limit” Physical Review Letters, 106(24):240502, June 2011.
Alec M. Hammond, Ian W. Frank, Ryan M. Camacho, "Error Correction in Structured Optical Receivers," IEEE Journal of Selected Topics in Quantum Electronics, 24, 1 (2018).